Classifying Control Systems

Let’s start with some simple nomenclature. Processes (i.e. reactors, filters) are controlled by controllers that consume measurements from sensors (i.e. flowmeters, analyzers) that monitor critical process states (i.e. flowrates, temperature, pressure) in real-time, as shown in Figure 1.

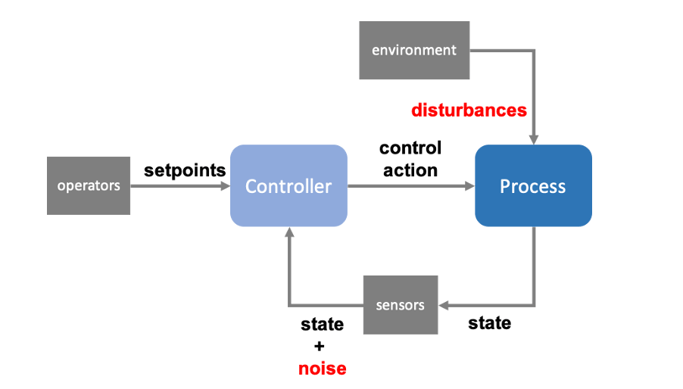
These controllers use these measurements to produce control actions (i.e., open/close valves, turn pumps on/off) in real time. A controller can be classified as either reactive or predictive based on the mechanism of how they consume these sensor measurements and generate control actions. Control actions in a reactive control system are based only on current or past states, i.e. current or recent sensor measurements of the process. Conversely, predictive controllers use predictions of the future state of the process to generate control actions, often employing some form of mathematical optimization and simulation model of the system.

Some examples of reactive controllers include variants of Proportional controllers, such as Proportional Integral (PI) and Proportional Integral Derivative (PID); whereas Model Predictive Control (MPC) is an example of predictive control strategies.

Proportional-Integral Derivative (PID) Control

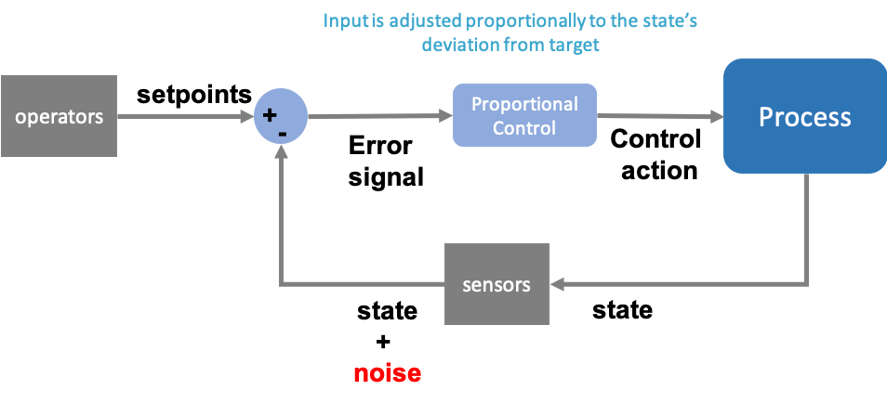
The most common reactive control (also known as feedback control) strategy applied in industrial and utility processes is the Proportional Integral Derivative (PID) controller. In a PID controller, the control action is a function of the measured state’s deviation, commonly referred to as “error”, from a desired setpoint (i.e. target), as shown in Figure 2. This target setpoint is typically specified by the human operator in order to achieve some production or compliance goal.

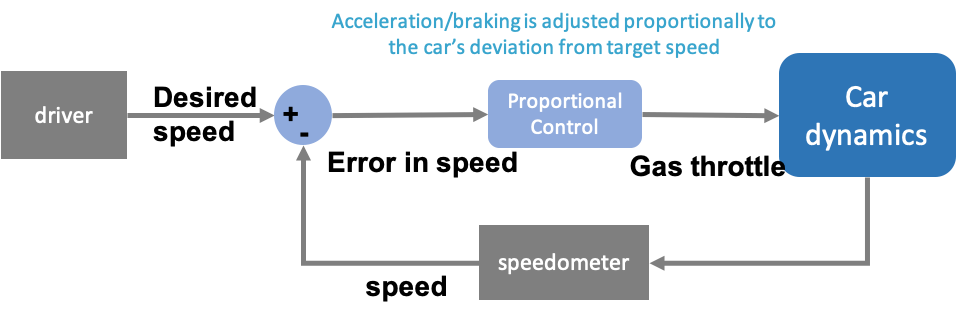
A common example of a PID controller is a simple car cruise control system, as shown in Figure 3. Here the driver (operator) specifies a desired speed (setpoint) and the controller calculates the corresponding acceleration required based on the difference between the current speed (as displayed on the speedometer) and the desired speed.

Each letter in the PID acronym denotes a “corrective mode” used by the controller to compute how the control action will respond to the deviation of the current state from its target, as shown in Figure 4. “Proportional” correction implies that the control action is computed as the immediate or linear response to the error, whereas “Integral” correction implies that the control action is computed as a function of the cumulative error of the state over a period of time. It is referred to as “Integral” control because the cumulative error over time is calculated using integration. Lastly, “Derivative” correction uses the rate of change of the states’ error, as measured by its derivative. As such, any reactive controller can be any combination of these calculations (PI, PID, or P).

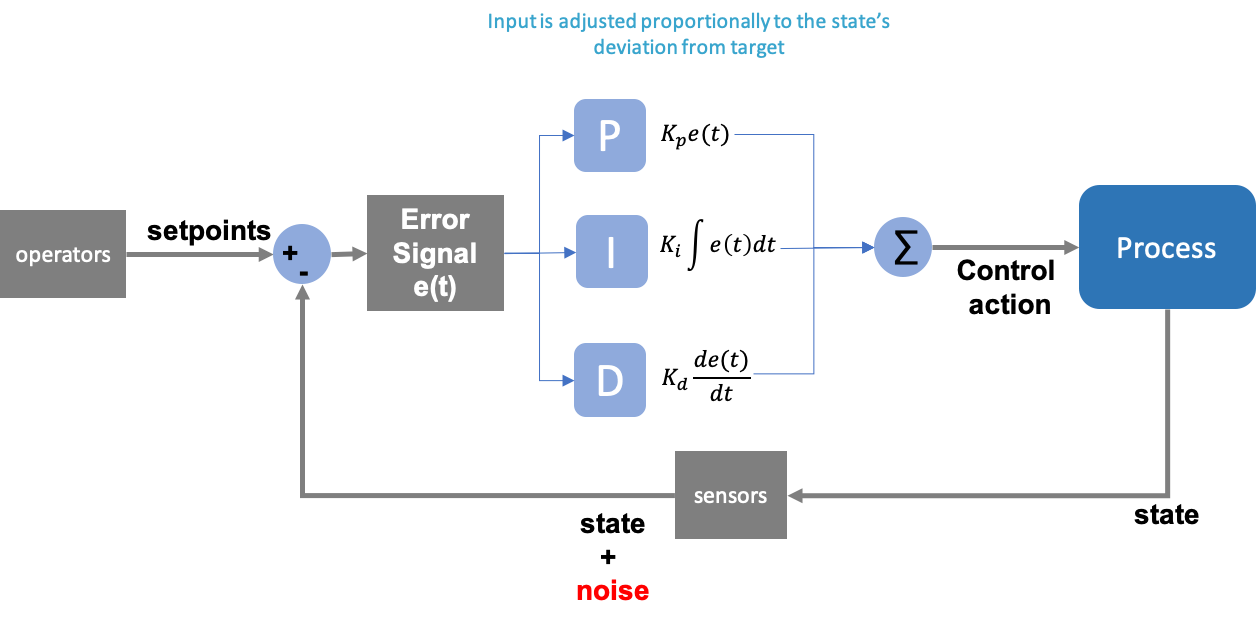
As shown in Figure 4, each corrective response is scaled by constants such as KP and KI, known as gain coefficients. These are parameters that are typically tuned by automation or control engineers. The controller gain can be adjusted to make the controller output changes as sensitive as desired to deviations between the setpoint and state variable; and the sign of coefficients can be chosen to make the controller output increase or decrease as the error signal increases.

Incorporating the derivative and integrative corrective modes as part of the controller depends on the type of process that is being controlled. The integrative correction ensures that long-term sustained deviations or error drifts do not occur, meanwhile the derivative correction ensures that the controller responds quickly to error changes, ensuring the controller doesn’t overshoot (overcompensate) in its response.

While reactive control strategies are very simple to formulate and deploy, its Achilles heel may have already become apparent. The control response of reactive controllers is continuously reacting to the current state of the system and has no foresight of its future dynamics. This means the controller is vulnerable to continuously evolving system behaviour or anomalies.

For industrial plants that are under highly competitive manufacturing environments, or utility systems that are stressed by climate change, constantly changing dynamics may be an everyday reality. For instance, if a large nutrient load hits a bioreactor, the system would expend significant energy to drive the dissolved oxygen back to the desired operating range. Alternatively, a pump may transition its status between online and offline many times within a given control horizon, to ensure that a downstream tank is within its operating range, thus leading to potential faults from undesirable pressure transients.

Model Predictive Control

The disadvantages listed above is precisely why Model Predictive Control (MPC) exists. MPC is a method designed for the proactive control of complex, nonlinear processes. While reactive-based control strategies, such as PID control, base their control actions on historical and current system states, as recorded by sensors, MPC uses predictions of future states. As such, an MPC controller requires an accurate simulation model of the process in order to generate reliable predictions.

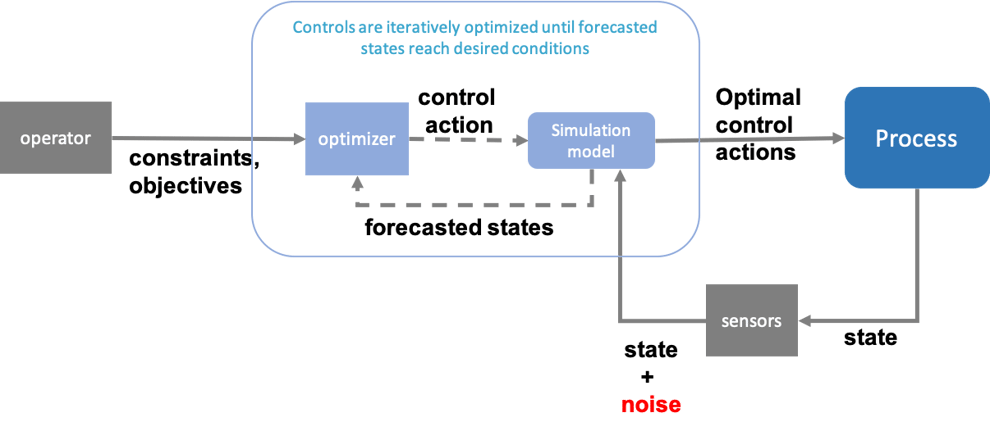
As shown in Figure 5, there are a few additional components that constitute an MPC that did not exist in a conventional reactive controller. These include:

1. simulation model: a mathematical representation of the process dynamics, i.e. it can predict what the future state of a process will be based on various control action sequences
2. optimizer: a mathematical solver that can iteratively determine the “optimal” control action based on outputs from the simulation model
3. constraints: specifies the boundary of acceptable future states that the optimizer cannot exceed, i.e. a compliance limit on ammonia discharge concentrations
4. objectives: the optimization goal the operator seeks to achieve, i.e. reducing energy costs

Predictive control operates by performing dynamic, real-time optimization to generate control actions that are adaptive to disturbances and compliant with user-specified constraints. MPC allows operators to run their processes more efficiently by operating much closer to constraints than would be possible with conventional reactive controllers.

The block diagram in Figure 5 provides a conceptual overview of the MPC framework. While the MPC structure is more complex than a conventional reactive controller, it offers several important advantages:

1. control actions are optimized to achieve a desired outcome, such as reducing energy costs or improving reaction efficiency
2. the controller is less sensitive to upsets from disturbances since it can anticipate them and respond faster
3. constraints on states and controls can be imposed on the controller to ensure compliant control actions are generated
4. accurate model predictions can provide early warnings of potential problems
5. the process model captures the dynamic interactions between control, state, and disturbance variables

Learning More

If you're interested in learning more about industrial process control systems and how companies like Basetwo are helping manufacturers optimize these control systems, feel free to check out our use cases and white papers on our resource page.